极大似然估计

0 前言

这是高数下册里面学到的知识，我印象中当时是比较简单的，做题的话套公式就可以了，但是在近期和一位师妹的学习沟通过程中，她问到了我很多细节，例如为什么在全连接层后面要用 softmax 函数呢？为什么 softmax 函数需要用指数的形式呢？我发现我检索到的很多回答很多都用到了极大似然估计的内容，好好再回顾以下相关的知识，记录于此。

值得注意的是，我们要把动机和优点区分开。动机是做这件事情的目的，优点是在完成这个目的时各个工具的优劣性，这两者不能混淆。例如：

• 在全连接层后使用 softmax 的动机是为了将全连接层的输出映射成一个概率分布。
• 那为什么现在常用的是 softmax 呢，其他的映射函数是否可以呢？
• softmax 这么常用，其优点又是什么呢？
• 在什么样的场合我们可以使用其他的映射函数呢？

私以为，这确实是一个研究生应当弄清楚的深度学习的理论基础，这有助于我们在今后撰写代码时不仅仅是网格搜索式地调参及改模型，也感谢我的师妹给我提了个醒，和我沟通确实有助于我进行知识的查漏补缺，让基础更加扎实一些。

01、什么是极大似然估计？

极大似然估计（Maximum Likelihood Estimate, MLE），是参数估计的一种方法。

• 参数估计的解释是：已知某个随机样本满足某种概率分布，但其中的参数不确定。参数估计就是通过若干次实验，观察其结果，利用结果推出参数的大概值
• 极大似然估计的思想：已知某组参数能够使得这个样本出现的概率最大，我们就将该组概率作为该组估计的真实值。
• 极大似然估计的优点
  • 渐进正确性：随着样本量的增加，估计值会最终趋向于真实值
  • 渐进正态性：估计的抽样分布服从正态分布
  • 有效性：极大似然估计在所有无偏估计中具有最小方差
• 极大似然估计的局限
  • 是一种粗略的数学期望
  • 一旦使用极大似然估计法，数据的产生过程必须严格完整地被假定并且描述，这意味着估计者需要对数据的产生过程有着较深的理解
  • 极大似然估计一般不太适用于包含理性预期的结构模型，这类模型中的似然函数通常高度非线性化，这使得模型的估计应为搜索全局最优而变得及其困难复杂

02、如何计算极大似然估计呢？

求解极大似然函数估计的一般步骤，在印象中这也是高数里面的解题方法，套路性非常强，当时以为是送分题（

• 写出似然函数
• 对似然函数取对数并整理
• 求导数
• 解似然方程

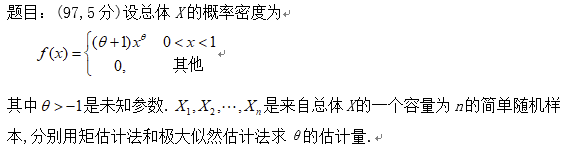
那么我们来解一道考研例题吧！

似然：理念世界和现实世界

似然值：从真实世界估计的参数下的真实事件发生的概率

神经网络本质上就是计算神经网络里面的概率模型的似然值，找到那个极大似然值所对应的概率模型，应该就是最接近现实情况的那个概率模型